Proponowana w artykule procedura pomiaru bokeh składa się z dwóch etapów: akwizycji obrazów i ich analizy numerycznej. W poniższych punktach opisujemy oba te elementy.

3.1 Akwizycja obrazów

W pierwszym kroku musimy uzyskać jądro K splotu. Dla wyidealizowanego aparatu o nieskończonej rozdzielczości i nieograniczonym zakresie dynamiki, jądrem splotu byłby nieostry obraz nieskończenie małego punktu. W świecie rzeczywistym aproksymujemy go robiąc w kontrolowanych warunkach zdjęcie punktowego źródła światła. W przykładach towarzyszących artykułowi użyto w tym celu diody LED.

Następujący wzór (zob. np. [Ray02]) podaje przybliżoną średnicę obrazu punktowego źródła światła rejestrowanego za pomocą obiektywu o ogniskowej f dla wartości przysłony N:

gdzie S₁ oznacza odległość obiektywu od płaszczyzny ostrości, zaś S₂ odległość od źródła światła. Wzór ten jest używany przez kalkulatory głębi ostrości, gdzie za c przyjmuje się średnicę krążka rozproszenia. W naszym jednak przypadku, oczekujemy, iż c będzie na tyle duże aby jądro splotu poddawało się analizie. Załóżmy, że sensor aparatu składa się z X × Y kwadratowych pikseli ułożonych w postaci siatki prostokątnej o wymiarach W × H milimetrów. Jeśli teraz oczekiwanym rozmiarem jądra jest d pikseli, to c = d · W/X. Traktując S₂ jako ustalony parametr, możemy rozwiązać równanie (2) ze względu na S₁:


Procedura akwizycji obrazów okazuje się być więc zbliżona do stosowanej w przypadku pomiaru komy obiektywu. Wszystko czego potrzebujemy, to stabilnie zamocowany aparat wraz z badanym obiektywem oraz dioda LED umieszczona przed obiektywem w ustalonej odległości S₂:


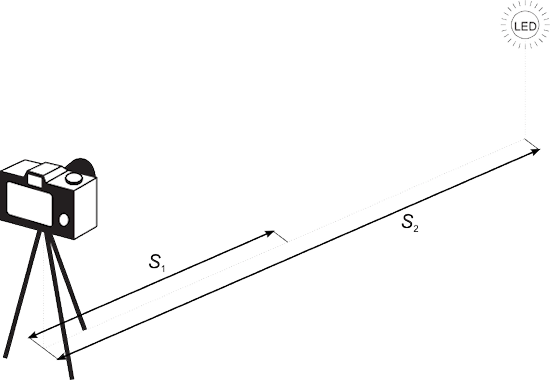
Ustawiając ostrość obiektywu na punkt odległy o wyliczoną wartość S₁ otrzymujemy nieostry obraz punktowego źródła światła, stanowiący dane wejściowe do analizy numerycznej opisanej w następnym podrozdziale. Bokeh może być zróżnicowany w różnych obszarach obrazu, zatem należy wykonać zdjęcia diody zarówno umieszczonej na osi optycznej obiektywu jak również blisko krawędzi bryły widzenia. Ponieważ wraz z przymykaniem przysłony charakter rozmycia obrazów pozaogniskowych może ulegać zmianie, procedurę należy powtórzyć dla różnych wartości przysłony.

----- R E K L A M A -----

NOWOŚCI OD LEICA DOSTĘPNE W E-OKO

Leica M11-P Edition Safari

41999 zł

Leica M11 Glossy Black

41499 zł

Leica 50/1.2 NOCTILUX-M ASPH. Glossy ...

36499 zł

Leica Q3 43

29900 zł 28498 zł

Kupujemy używany sprzęt za gotówkę. Raty 20x0%!

3.2. Przetwarzanie obrazów

Z poprzedniego kroku otrzymaliśmy zdjęcie cyfrowe w postaci macierzy P = [p(x,y)] o wymiarach X × Y pikseli. Zakładamy przy tym, że elementy macierzy są znormalizowane do przedziału jednostkowego [0,1], gdzie 0 oznacza czerń, zaś 1 biel. Na zdjęciu tym zarejestrowany jest nieostry obraz punktowego źródła światła mający średnicę około d pikseli. Proponowana procedura analizy bokeh składa się z następujących etapów, które kolejno omówimy:

1. odszumienie obrazu;
2. wyznaczenie centroidu;
3. obcięcie obrazu;
4. przejście do współrzędnych biegunowych;
5. wyznaczenie współczynnika CD (odstępstwa od symetrii kołowej);
6. kompensacja odstępstwa od symetrii kołowej;
7. wyznaczenie współczynnika MV (odstępstwa od monotoniczności).

1. Pierwszym krokiem jest odszumienie obrazu, gdyż szum (zwłaszcza w dominujących ciemnych partiach zdjęcia) może znacząco zafałszować wyniki dalszych obliczeń, a w szczególności wyznaczenie współrzędnych centroidu. Ilość znanych algorytmów odszumiania obrazów cyfrowych jest obecnie niemała, poczynając od zwykłego odcięcia aż po metody z zakresu analizy falkowej (por. np. [BCM05]).

2–3. W następnym etapie następuje obcięcie macierzy P do kwadratowego sąsiedztwa centroidu obrazu źródła światła. Współrzędne (x_c, y_c) centroidu wyznaczamy jako środek ciężkości binaryzacji macierzy P (por. np. [Jah05, rozdz. 19, par. 3]):

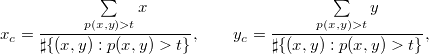
gdzie t jest parametrem binaryzacji zapewniającym wydzielenie obrazu źródła światła z tła. Jądro splotu K= [k(x,y)] jest wycinkiem kwadratowym o boku 2δ obrazu P scentrowanym w punkcie (x_c,y_c). Oczywiście 2δ > d (w przykładach na końcu artykułu użyto δ = d):

4. Następnym etapem jest przekształcenie jądra do współrzędnych biegunowych, otrzymujemy w ten sposób nową macierz K₁ = [k₁(r,φ)] za pomocą wzoru:

gdzie przez oznaczamy ciągłą rekonstrukcję sygnału dyskretnego K. (Rekonstrukcja sygnału i jego powtórne próbkowanie, a w pewnych sytuacjach również użycie filtra dolno-przepustowego służą uniknięcia efektu aliasingu. Więcej na temat transformacji geometrycznych obrazu cyfrowego można znaleźć w [BB09] oraz [Jah05]).

5. Teraz, wykorzystując wybrany algorytm wykrywania krawędzi, dla każdego kąta φ wyznaczamy odpowiadający mu promień r_φ tak, aby zbiór { k₁(r_φ, φ): φ ∊ [0,2π) } tworzył krawędź obrazu źródła światła (a więc nośnika jądra). Współczynnik CD wyznaczamy teraz ze wzoru (1). Przypomnijmy:

6. Naszym kolejnym celem jest określenie uśrednionego przebiegu zmienności natężenia światła wzdłuż promienia jądra. W tym celu dokonujemy wyrównania promieni dla wszystkich wartości φ. Pamiętając, że operujemy na obrazie przekształconym do współrzędnych biegunowych, jedyne co należy zrobić, to przemnożyć każdą kolumnę macierzy K₁ przez współczynnik E(r_φ )/r_φ , gdzie φ oznacza kąt odpowiadający danej kolumnie. Otrzymujemy w ten sposób nową macierz K₂ = [k₂(r,φ)] (jak poprzednio, _1,φ oznacza ciągłą rekonstrukcję sygnału dyskretnego kolumny macierzy K₁ dla kąta φ):

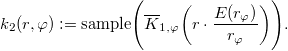
W efekcie powyższych zabiegów, obraz diody zajmuje pierwszych E(r_φ) wierszy macierzy K₂.

7. Średni przebieg zmienności intensywności światła wzdłuż promienia jądra otrzymujemy wyznaczając średnią z każdego wiersza macierzy K₂:

Jeżeli teraz oznaczymy przez J(r) minimalną intensywność światła w kole o promieniu r, czyli J(r) := min{ I(s): s ≤ r }, to współczynnik MV definiujemy jako odległość (w normie ℓ1) funkcji intensywności od J, przeskalowaną dodatkowo o czynnik 1/E(r_φ), aby uniezależnić wynik od uzyskanej faktycznie średnicy obrazu źródła światła: