Zestaw pierścieni pośrednich Photoolex

1/f = 1/x + 1/y.

Tak przedstawione równanie możemy odczytać w następujący sposób: odwrotność ogniskowej jest równa sumie odwrotności odległości obrazowej oraz przedmiotowej. Najlepiej zrozumieć to, analizując podstawowy schemat pracy soczewki:

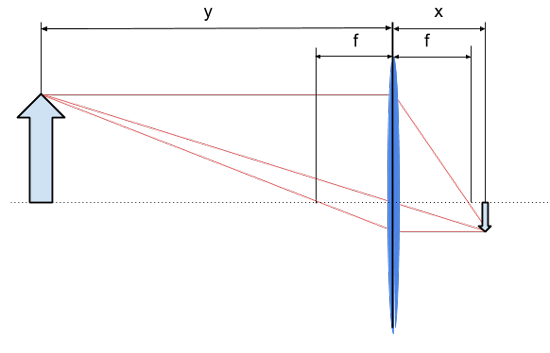
Gdy od naszego motywu, strzałki stojącej w odległości y, poprowadzimy trzy promienie tak, by jeden z nich był prostopadły do soczewki, a dwa kolejne przechodziły przez ognisko soczewki oraz jej oś optyczną, po drugiej stronie soczewki w ten sam sposób będziemy dalej kreślić linie, w miejscu ich przecięcia będzie obraz naszej strzałki: rzeczywisty i odwrócony. Stosunek wartości obu odległości, przedmiotowej i obrazowej, to skala odwzorowania S = x/y, popularnie zwana powiększeniem. Skala ta zwyczajowo podawana jest jako stosunek, np. 1:5, który oznacza, że obraz o wielkości jednostkowej (bez względu na użytą jednostkę) przedstawia przedmiot pięć razy większy.

----- R E K L A M A -----

PROMOCJA SONY - 50% RABATU NA OBIEKTYW!

Sony A7 IV + 24-70/4 FE ZA OSS

15122 zł 13710 zł

Sony A7 IV + 50/1.8 FE

13146 zł 12722 zł

Sony A7 III + 24-70/4 ZA FE OSS

10822 zł 9410 zł

Sony A7 III + 50/1.8 FE

8846 zł 8422 zł

Jeśli w odległości x umieścimy matrycę aparatu fotograficznego, będziemy mogli powyższy rysunek uznać za schemat pracy aparatu fotograficznego. To, że obraz strzałki jest pomniejszony nie powinno nam przeszkadzać. Wszak matryce w aparatach nie mają dużych gabarytów. Co jednak się stanie, gdy chcielibyśmy fotografować detale i uzyskiwać znaczne powiększenie? Nic trudnego – wystarczy przysunąć się bliżej do motywu.

Sposób prowadzenia linii jest taki sam – jedna prostopadła do soczewki, jedna przecinająca ognisko, a kolejna to oś optyczna. Pojawił się nowy obraz rzeczywisty i odwrócony, jednak tym razem zdecydowanie większy.

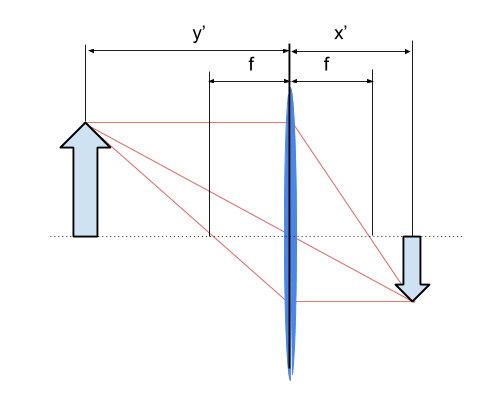
Faktycznie, ze wzoru odczytać możemy, że przy rygorze utrzymania tej samej ogniskowej, zwiększanie jednej wartości odległości będzie wymagało zmniejszenia drugiej. Możemy też znaleźć punkt „równowagi”, gdzie x = y.

Zwróćmy uwagę na to, że na drugim rysunku odległość od matrycy oznaczona jest jako x′. Dlaczego? To właśnie sposób działania soczewki. Ponieważ x′ > x, powiększony obraz pojawi się… za matrycą. Innymi słowy nie uzyskamy ostrego zdjęcia. Faktycznie – gdy nie zmieniamy parametrów obiektywu, to znaczy nasze f jest stałe, każde przesunięcie tegoż obiektywu bliżej lub dalej motywu spowoduje wytworzenie obrazu w innej odległości od matrycy. Jak z tym problemem radzimy sobie w fotografii? Po prostu odsuwamy soczewkę od matrycy (zwiększamy x), kompensując w ten sposób różnicę w odległości obrazowej. Ta operacja nie jest wprost widoczna – w niektórych obiektywach jednak zmniejszanie odległości ostrzenia z nieskończoności ku wartości minimalnej powoduje, że cały zespół soczewek wyraźnie odsuwa się od aparatu. Ważne, by pamiętać, że taki obiektyw nie zmienia ogniskowej.

Klasyczne „ostrzenie” przez odsuwanie zespołu soczewek od matrycy

Konstrukcja obiektywu narzuca nam dopuszczalny zakres nastawy odległości przedmiotowej. W jednym minimalna jej wartość będzie wynosić 20 cm, w drugim 60 cm, a w jeszcze innym 1.5 m. Weźmy dla przykładu popularny i tani model Nikkor AF-D 50mm f/1.8. Jego minimalna odległość ostrzenia to 45 cm, a skala odwzorowania to 1:6.8. Stosunkowo mały wynik.

Makrofotografia to technika fotografowania przy skalach odwzorowania większych od 1:1. Innymi słowy dążymy do tego, by przedmiot wielkości 1 cm na matrycy aparatu nie zajmował więcej niż 1 cm. Jak możemy zmusić wspominanego Nikkora, by z dostępnej skali 1:6.8 uzyskać przynajmniej 1:1? Musimy go jeszcze bardziej odsunąć od matrycy. W tym celu użyjemy mieszka lub pierścienia pośredniego, czyli akcesorium, które mocujemy pomiędzy obiektywem a aparatem fotograficznym. Spowoduje ono jedynie zwiększenie odległości obiektywu od matrycy.

Mieszek fotograficzny

Pierścienie pośrednie

Wróćmy na chwilę do wzoru soczewki. Łatwo zauważyć, że po wyostrzeniu obrazu na nieskończoność (y → ∞) odległość soczewki od matrycy będzie równa ogniskowej soczewki. Gdy ostrzymy na bliższe przedmioty, musimy tę odległość zwiększyć o dodatkowy wyciąg x = f + d. Równanie przyjmie postać:

1/(f+d) + 1/y = 1/f
lub inaczej
1 + (f+d)/y = (f+d)/f.

Widzimy też, że (f+d)/y to nic innego jak skala odwzorowania, zatem

1 + S = (f+d)/f

lub po przekształceniu

S = d/f.

Oznacza to, że chcąc uzyskać odpowiednią skalę odwzorowania, musimy odsunąć obiektyw od położenia odpowiadającego nieskończoności o odległość d. Dla skali 1:1 otrzymujemy d = f. Innymi słowy, by uzyskać skalę 1:1, obiektyw o ogniskowej 50 mm musimy odsunąć o 50 mm.

Historycznie mieszek był pierwszym stosowanym w fotografii elementem dającym kontrolę nad odległością soczewki od kliszy filmowej. Mimo niewątpliwych zalet jego użycie nie jest zbyt wygodne. Przyrząd ten nie sprawdza się w każdych warunkach (np. deszcz może zniszczyć konstrukcję ożebrowania miecha). Pierścień pośredni możemy traktować jako mieszek o ustalonym wysuwie, a mieszek – jako elastyczny pierścień. To de facto jedyna różnica między tymi dwoma przyrządami (prócz wspomnianej wyżej odporności na warunki użytkowania).

Zestaw pierścieni pośrednich Photoolex o rozmiarach 13, 21 oraz 31 mm

Pierścienie są małe, lekkie i możliwe do użycia w sytuacjach, w których mieszek mógłby nie podołać. Kolejny ważny aspekt: użycie pierścieni nie wymaga od nas natychmiastowego zastosowania solidnego statywu, tak jak w wypadku mieszka. Możemy je stosować z każdym rodzajem obiektywu – nawet makro. Jedynym minusem jest konieczność demontowania obiektywu, gdy chcemy zmodyfikować wysuw.

Pierścień pośredni Photoolex zamontowany na aparacie fotograficznym

Ważną cechą jest brak jakichkolwiek elementów optycznych – pierścień jest w uproszczeniu tuleją dystansową. To daje gwarancję, że w przeciwieństwie do soczewek nasadkowych czy telekonwerterów w torze optycznym nie znajduje się żaden dodatkowy element mogący negatywnie wpływać na jakość obrazu.

W praktyce prostą metodą na oszacowanie skali uzyskanej kombinacją nastawy obiektywu i pierścieni jest nie liczenie ze wzorów, ale sfotografowanie papieru milimetrowego. Wystarczy odczytaną odległość w poziomie z fotografii podzielić przez wielkość sensora aparatu jakim dysponujemy.

Pomiar skali odwzorowania używając papieru milimetrowego

W przykładzie powyżej widzimy, że na zdjęciu został zarejestrowany obszar o rozmiarze poziomym 26 mm. Używaliśmy aparatu pełnoklatkowego, czyli odpowiadający rozmiar matrycy to 36 mm. Zatem użyta skala odwzorowania to S=36/26, czyli 1.4:1.